这是 Reach-Top 2385 题的题解，翻译自 Codeforces。

因为被各种自己瞎倒腾都只能收获TLE，所以查了一些资料，了解到了这个名为Manacher的算法，忍不住就打算写篇博客记录一下。

概述 链接到标题

这是一个专门用来处理最长回文子串的算法，主要思想是：遍历每个串中的每个字符，且将其定为一个回文串的中心，并向两边扩展，以此寻找最长回文子串。但需要关注的是偶数个数的子串无法直接使用该法，所以在算法中我们先预处理一下字符串，使其的回文子串全部变成奇数个数的。

1.预处理 链接到标题

首先算法提供了一个巧妙的办法：在相邻两个字符间插入一个不会出现在原串中的字符串（一般为 # ），同时首尾也各加一个。

例如：

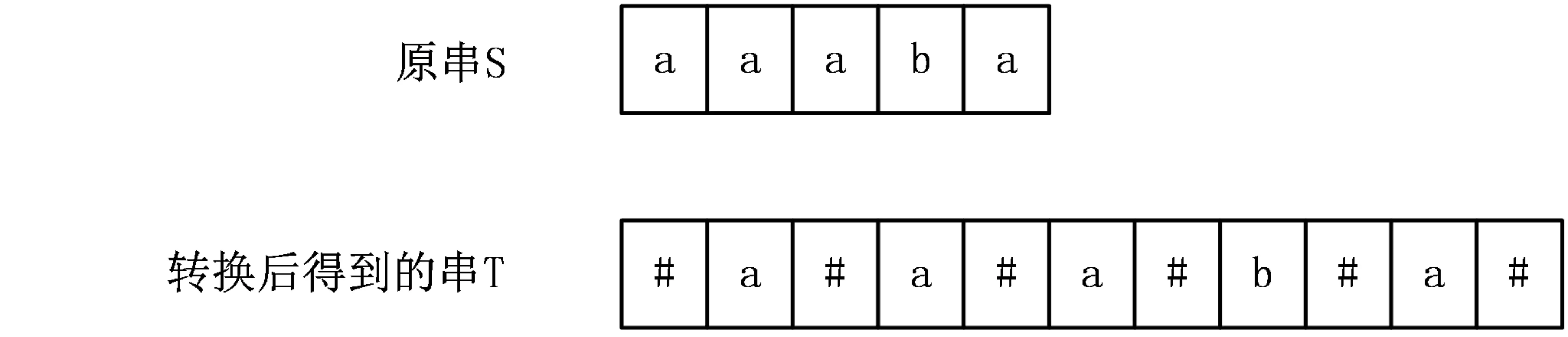
2.Len数组 链接到标题

简介 链接到标题

Len[i]用于表示以字符T[i]为中心的最长回文子串右边界到T[i]的长度，比如以T[i]为中心的最长回文子串是从T[l]到T[r]，那么Len[i]=r-i+1。

于是对于上面给出的例子，我们可以得出Len数组为：

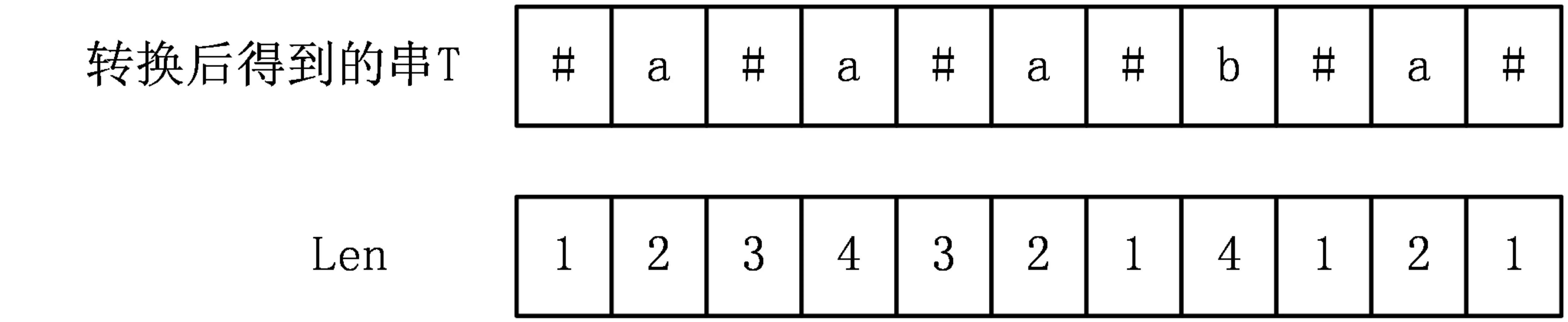
性质 链接到标题

Len[i]-1 = 该回文子串在原字符串S中的长度

证明：

已知字符串T中所有的回文子串长度都为奇数，那么对于以T[i]为中心的最长回文子串，其长度就是2*Len[i]-1。

根据预处理的方法可以知道，分隔符 # 的数量一定比其他字符的数量多1，所以该最长回文子串中有Len[i]个分隔符 # 和Len[i]-1个其他字符。

3.计算Len数组 链接到标题

有了上面的性质，题目变转化为了求所有的Len[i]，然后找出最大值输出即可，下面介绍如何在线性时间复杂度内求出结果。

因为是从左往右计算，所以当我们计算Len[i]时，Len[j]（0 <= j < i)就已经计算好了。

设P为已计算的最长回文子串的右边界中的最大值，Po为P所在的最长回文子串的中心，那么计算Len[i]就可以分成两种情况了：

第一种情况： i <= P 链接到标题

通过回文字符串的定义我们可以知道在Po的左边距离等于i-Po的地方找到一个j，这个j和i存在一定的关系。

Len[j] < P - i 链接到标题

这时的情况如下图：

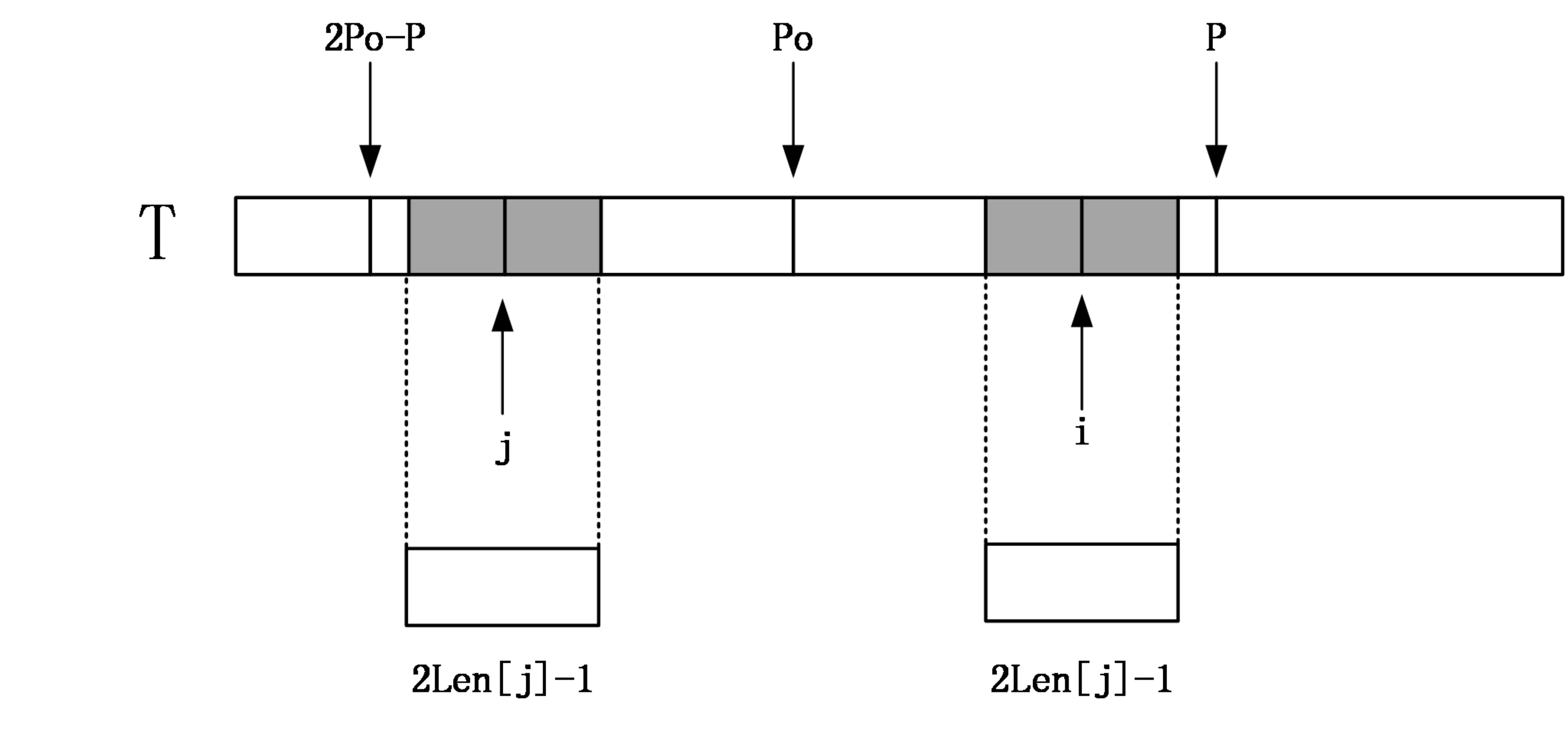
因为以T[i]、T[j]为中心的回文子串都在以T[Po]为中心的最长回文子串中，所以很显然此时Len[j]=Len[i]。

Len[j] >= P - i 链接到标题

此时的情况如下图：

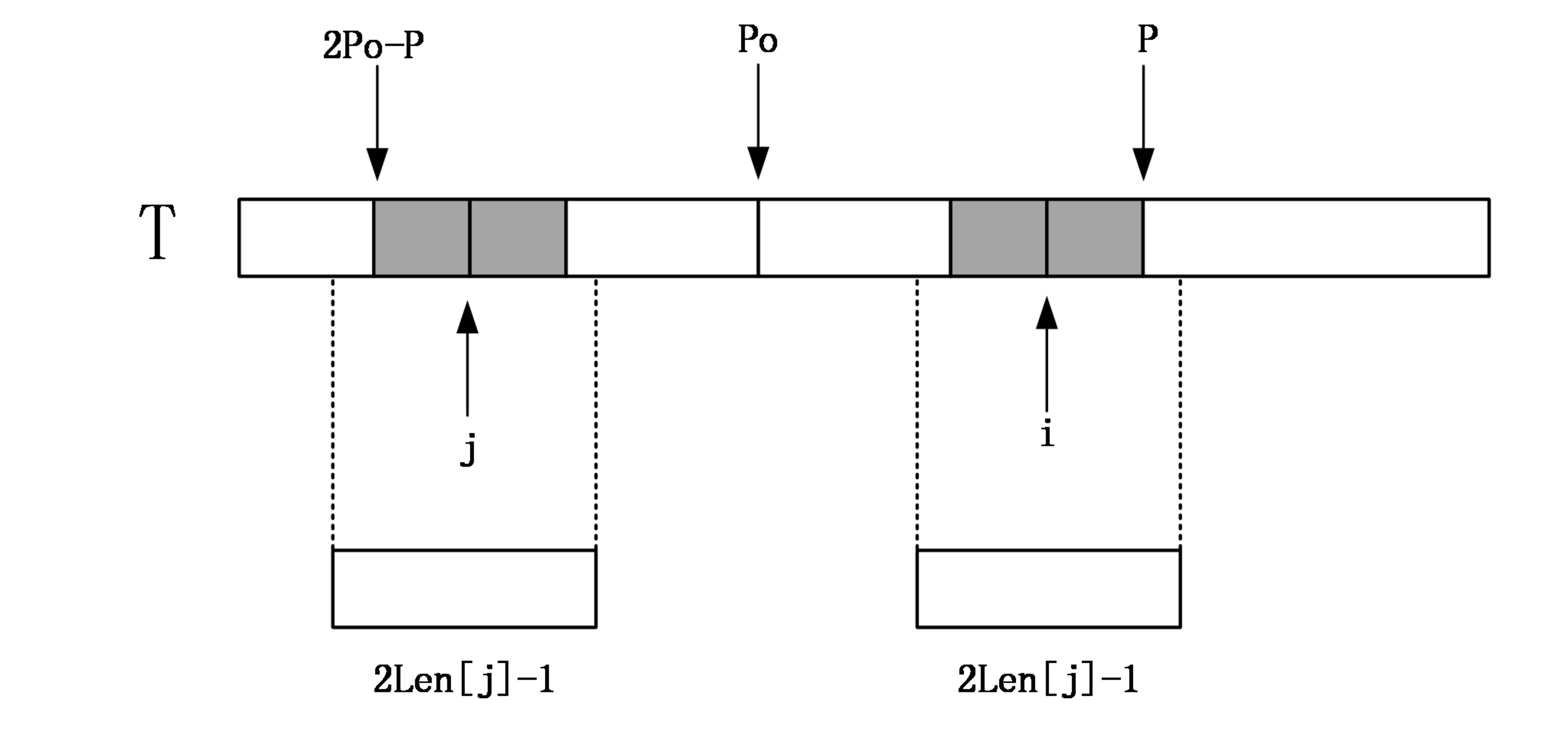
P的右侧是我们还没有匹配过的区域，所以要从P+1的位置开始进行对应匹配，直到发生失配，此时以Len[i]为中心的最长回文子串的右边界已经在P右侧了，所以P、Po都需要更新了。

第二种情况：i > P 链接到标题

在这种情况下以T[i]为中心的回文串还一点都没匹配过，只能老老实实匹配了，发生失配后也要更新P和Po。

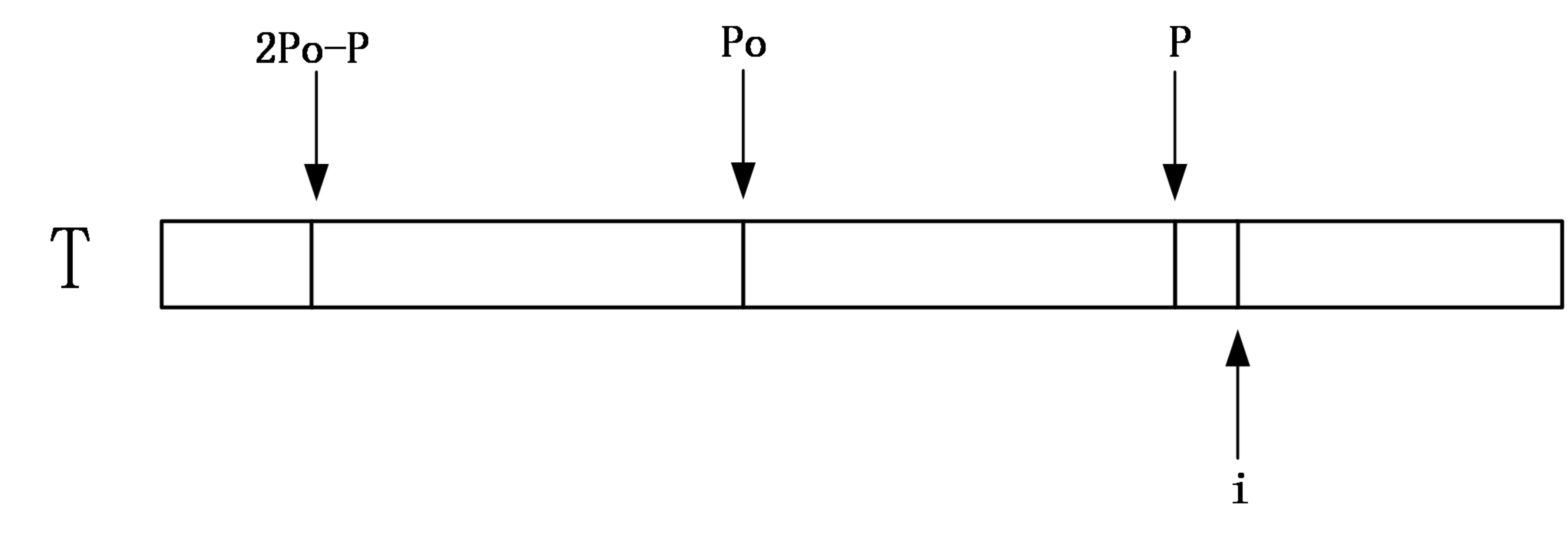
4.时空复杂度 链接到标题

时间复杂度 链接到标题

我们从上面的Len数组计算中可以知道算法只在没匹配过的地方进行匹配，而已经匹配过的地方是不需要重新匹配的，因此时间复杂度是线性的。

空间复杂度 链接到标题

显然这是将空间扩大了一倍，为O(2n).

5.代码 链接到标题

这里我在字符串T的最前面加了一个特殊字符 $ 来避免频繁更新P的时候导致数组越界。

#include<bits/stdc++.h>
using namespace std;
int main() {
    int n;
    string S;
    while(cin >> S) {
        string T = "$#";
        for(int i = 0; i < S.size(); i ++) {    //预处理字符串
            T += S[i];
            T += "#";
        }
        vector<int> Len(T.size(), 0);   //辅助数组Len
        int Po = 0, P = 0, start = 0, maxLen = 0;
        for(int i = 1; i < T.size(); i ++) {
            Len[i] = i < P ? min(Len[2 * Po - i], P - i) : 1;
            while(i + Len[i] < T.size() && i - Len[i] > 0 && T[i + Len[i]] == T[i - Len[i]]) {  //这里进行匹配，注意别让数组越界
                Len[i] ++;
            }
            if(i + Len[i] > P) {    //更新P和Po
                Po = i;
                P = i + Len[i];
            }
            if(Len[i] - 1 > maxLen) {
                start = (i - Len[i]) / 2;
                maxLen = Len[i] - 1;
            }
        }
        cout << maxLen << endl;
    }
    return 0;
}