这是 Reach-Top 4626 题的题解，翻译自 Codeforces。

题目

本题适用十分经典的并查集算法，本文就整理一下这个经典算法。

概述 链接到标题

并查集是一种树形的数据结构，顾名思义是用来处理集合的合并与查询问题的

初始化 链接到标题

我们定义一个 fa 数组，用于记录数据i的祖先节点（或父节点），然后我们初始化 i 的父节点为 i 本身。

void makeSet(int size) {
    for(int i = 0; i < size; i ++) {
        fa[i] = i;
    }
}

查找 链接到标题

我们带入这样一个情形：如果两个人想看看自己祖上八百年是不是一家该怎么办？

他们想了这样一个办法，他们各自找出自己的父亲，然后再找出父亲的父亲，一直找下去，直到尽头，再看看他们找出来的高祖是不是同一个人，如果是的话那么真的太巧了，他们居然祖上八百年前是一家欸！

我们抽象成树形图就是这样的：

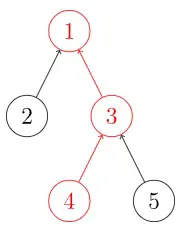
example1

我们可以依照查找思想发现 2 和 5 的祖先是同一个人。

int find(int x) {
    if(fa[x] == x)
        return x;
    else
        return find(fa[x]);
}

压缩路径 链接到标题

刚刚那两个人觉得这样查太墨迹了，还不如我直接认我高祖当爸爸了呢，甚至我们只需要随便找一个组长出来认他当爸爸就好了。把路径上的每个节点都直接连接到根上 ，这就是压缩路径。

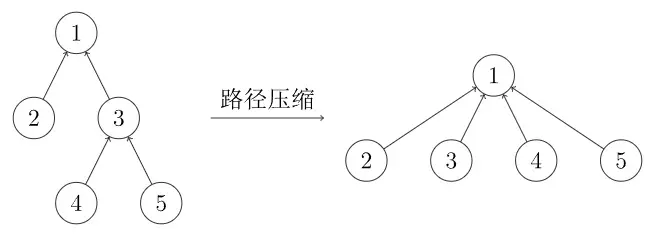
example2

int find(int x) {
    if(fa[x] != x)
        fa[x] = find(fa[x]);
    return fa[x];
}

合并 链接到标题

有两个不是一个家族的人要结成亲家了，他们想趁着这个机会让两个家族合并了，通过上面的压缩路径我们可以发现让甲家族的祖先认乙当爸爸的话两个家族就合并了。

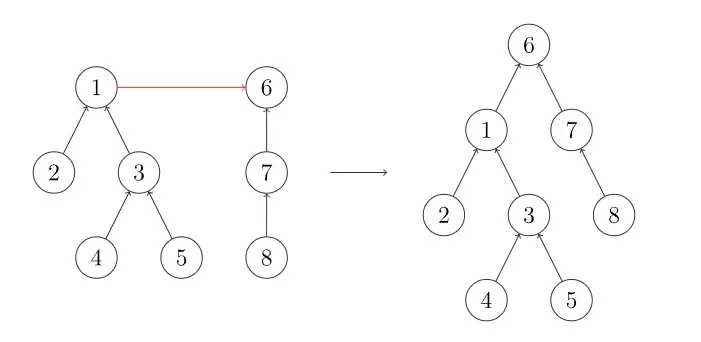
example3

void unionSet(int x, int y) {
    x = find(x);
    y = find(y);
    fa[x] = y;
}

启发式合并（按序合并） 链接到标题

刚刚那两个家族发现甲家族比乙家族大很多，让甲家族的人搬到乙家族来显然要比乙家族的人搬到甲家族去来的麻烦，所以他们就觉得让乙家族的人搬到甲家族来。

std::vector<int> size(N, 1);  // 记录并初始化子树的大小为 1
void unionSet(int x, int y) {
    int xx = find(x);
    yy = find(y);
    if (xx == yy) 
        return;
    if (size[xx] > size[yy])
        swap(xx, yy);
    fa[xx] = yy;
    size[yy] += size[xx];
}

时空复杂度 链接到标题

时间复杂度 链接到标题

同时使用路径压缩和启发式合并之后，并查集的每个操作平均时间仅为 O(α(n))，其中 α 为阿克曼函数的反函数，其增长极其缓慢，也就是说其单次操作的平均运行时间可以认为是一个很小的常数。

Ackermann 函数 A(m,n) 的定义是这样的：

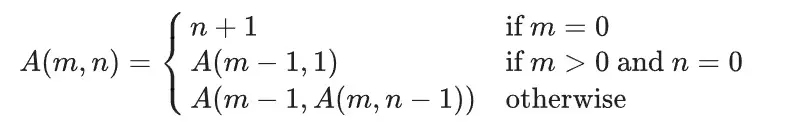
example4

而反 Ackermann 函数 α(n) 的定义是阿克曼函数的反函数，即为最大的整数m使得 A(m,m)≤n。

空间复杂度 链接到标题

显然为 o(n)。

带权并查集 链接到标题

我们还可以在并查集的边上定义某种权值、以及这种权值在路径压缩时产生的运算，从而解决更多的问题。比如对于经典的「NOI2001」食物链，我们可以在边权上维护模 3 意义下的加法群。

本题解法 链接到标题

我们可以运用并查集思想，将一对可以反应的物质中的第一个设为第二个的父节点，多次设立父节点，路径合并后就可以建立多个可以反应的树，因为题目只需要得出最危险的情况，所以我们可以认为除放入每个树的第一种物质以外，放入其他的物质都是可以反应的，就能轻松得出结果了。

#include<bits/stdc++.h>
using namespace std;
int fat[51];
int find(int x) {
    while(fat[x] != x) {
        x = fat[x];
    }
    return x;
}
int main() { 
    int n, m, a, b;
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) {
        fat[i] = i;
    }
    for(int i = 1; i <= m; i ++) {
        cin >> a >> b;
        if(find(a) != find(b))
            fat[find(b)] = find(a);
    }
    long long ans = 1;
    bool c[2001];
    memset(c, 0, sizeof(c));
    for(int i = 1; i <= n; i ++) {
        int k = find(i);
        if(!c[k]) {
            c[k] = 1;
        }
        else {
            ans *= 2;
        }
    }
    cout << ans;
    return 0;
}