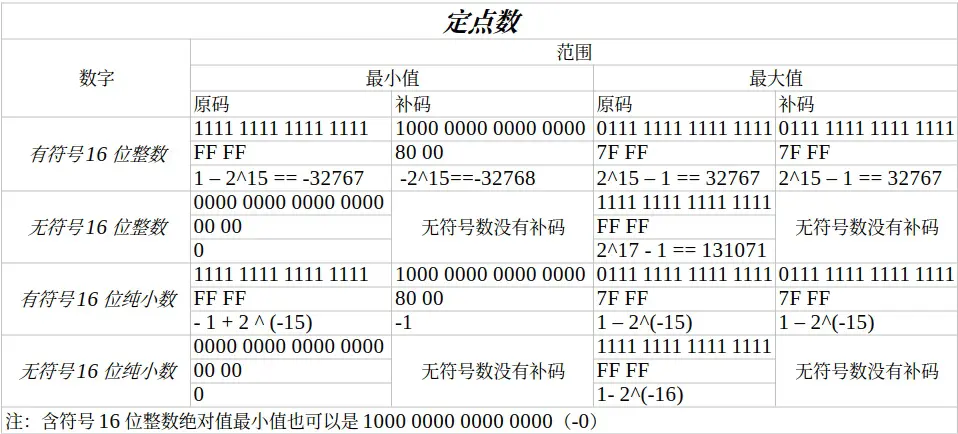
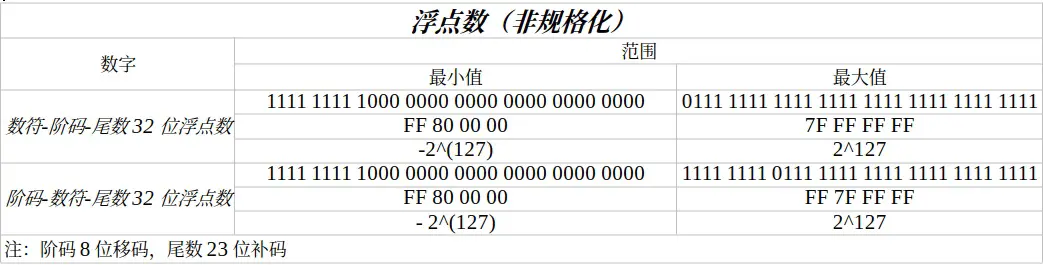
数字在计算机中的编码有原码、反码、补码、移码四种类型,每一种编码都有一定的作用,数字又有浮点数、定点数等类型,因此整理一下它们十分有必要。
基本概念 链接到标题
真值 链接到标题
人类表示数字的形式,可以是十进制也可以是二进制,负数前面有负号,例如 99D、-100B。
机器数 链接到标题
计算机存储数字的形式,只能是二进制的,如果需要的话可以用符号位来表示正负,例如 10010。
分为无符号数与带符号数两类,也可以分为定点数与浮点数两类。
符号位:计算机存储数字时用于表示正负的那一位,1 表示该数为负数,0 表示该数为正数。
无符号数 链接到标题
这种类型的数字只能是定点数,只能用原码表示,每一位都用于表示数字的大小,例如在八位系统下,10000000B = 128D。
整数 链接到标题
一般指带符号整数,即最高位为符号位的整数,有原码、反码、补码、移码四种编码形式,例如在八位系统原码表达下,1000001B = -1D。
定点数 链接到标题
一般指带符号纯小数,一般用原码或补码表示,例如在八位系统原码表示下,01000000B = 0.5D
定点指的是小数点的位置固定,一般为最低有效位之后(整数)或最高有效位之前(纯小数)。
浮点数 链接到标题
这一类数由阶码与尾数组成,类似人类的科学计数法,$N = 2^E * 0.M$
在本科阶段机组学习过程中,尾数是纯小数的形式,即 1000000 表示 0.10000000。但标准格式下不是这样的,详见 IEEE 754。
一般有以下三种组成形式:
- 阶码(移码)+ 尾数(移码)
- 阶码(移码)+ 数符 + 尾数(补码或原码)
- 阶符 + 阶码(补码或原码)+ 数符 + 尾数(补码或原码)
原码 链接到标题
最高位为符号位,有效位均用二进制真值表示。例如 $[01000000]_原$ = 64D、$[10000001]_原$ = -1D。
原码较多运用于乘除运算。
反码 链接到标题
正数的反码与对应的原码一致,负数的反码是在对应的原码的基础上除符号位外取反。例如 $[01000000]_反$ = 64D、$[11111110]_反$ = -1D。
需要注意的是反码中有 +0($[00000000]_反$)和 -0($[10000000]_反$)两个 0。
用的较少。
补码 链接到标题
正数的补码与对应的原码一致,负数的补码是在对应的原码基础上除符号取反加一得到的。例如 $[01000000]_补$ = 64D、$[11111111]_补$ = -1D。
在求负数补码时也可以简化为符号位与最低位开始的连续 0 与最低的 1 不变,其他位取反,例如 $[10001000]_原$ = $[11111000]_补$
$[10000000]_补$ 是一个特殊的数,它无法被同样宽度的原码表示,但却可以被补码表示。
补码可以避免反码两个 0 的问题,较多运用于加减运算。
移码 链接到标题
又叫增码或偏置码。
移码的数值位与对应的补码一致,符号位用 1 表示正数,0 表示负数。可以理解为以 $[10000000]_移$ 为轴大致对称的两部分。例如 $[11000000]_移$ = 64D、$[01111111]_移$ = -1D。
因为有像数轴类似的性质,所以移码较多运用于比较,即表示浮点数的阶码。
规格化 链接到标题
在浮点数中,为了在尾数中表示最多的有效数据位,同时使浮点数具有固定的表示方式,浮点数的编码应当采用一定的规范,即尾数调整到最高有效位与符号位相反。例如 $2^{100}*0.00100000$ 规格化后是 $2^{110}*0.10000000$。
这里又涉及到了移位操作,这个我们以后再讲。
取值范围 链接到标题