本文将从计组和汇编两个角度总结整理四则运算、逻辑运算、位运算。

约定链接到标题

本文使用的汇编指令集为 8086 计算机的汇编指令集；
所有定点数均为 8bit(2bit 数符)；
所有浮点数均为 8bit(1bit 数符 + 3bit 阶码(移码) + 4bit 尾码(补码))。

加、减法运算链接到标题

汇编指令链接到标题

操作符	操作数	执行的操作	描述
ADD	DST, SRC	(DST) <- (SRC) + (DST)	加法
ADC	DST, SRC	(DST) <- (SRC) + (DST) + CF	带进位的加法
INC	OPR	(OPR) <- (OPR) + 1	加 1
SUB	DST, SRC	(DST) <- (DST) - (SRC)	减法
SBB	DST, SRC	(DST) <- (DST) - (SRC) - CF	带借位的减法
DEC	OPR	(OPR) <- (OPR) - 1	减 1
NEG	OPR	(OPR) <- -(OPR)	求补
CMP	DST, SRC	(DST) - (SRC)	比较

以上指令影响标志位，但 INC 和 DEC 不影响 CF。

对以字为单位的数据进行计算链接到标题

;16bit 加法(RR)
ADD AX, BX
ADC DX, CX
;16bit 加法(RS)
MOV AX, addr
CWD
ADD AX, BX
ADC DX, CX
;16bit 加法(立即数)
ADD AX, 10H
ADC DX, 0

;16bit 减法(RR)
SUB AX, BX
SBB DX, CX
;16bit 减法(RS)
MOV AX, addr
CWD
SUB AX, BX
SBB DX, CX
;16bit 减法(立即数)
SUB AX, 10H
SBB DX, 0

;16bit 求补
NEG DX
NEG AX
SBB DX, 0

底层实现链接到标题

进行加减法的两个操作数是用补码形式存储的，这样就可以用同一套加法器硬件来实现定点正负数的加减法。

公式链接到标题

$[x]_补+[y]_补=[x+y]_补 (mod 2^{n+1})$

$[x-y]_补=[x]_补-[y]_补=[x]_补+[-y]_补$

移码的加减法公式：

$[x+y]_移=[x]_移+[y]_补$

$[x-y]_移=[x]_移+[-y]_补$

溢出检验链接到标题

$ovr=\bar{A_f}\bar{B_f}S_f+A_fB_f\bar{S_f}=C_f\oplus C_n=S_{f1}\oplus S_{f2}$

硬件链接到标题

FA: 全加器

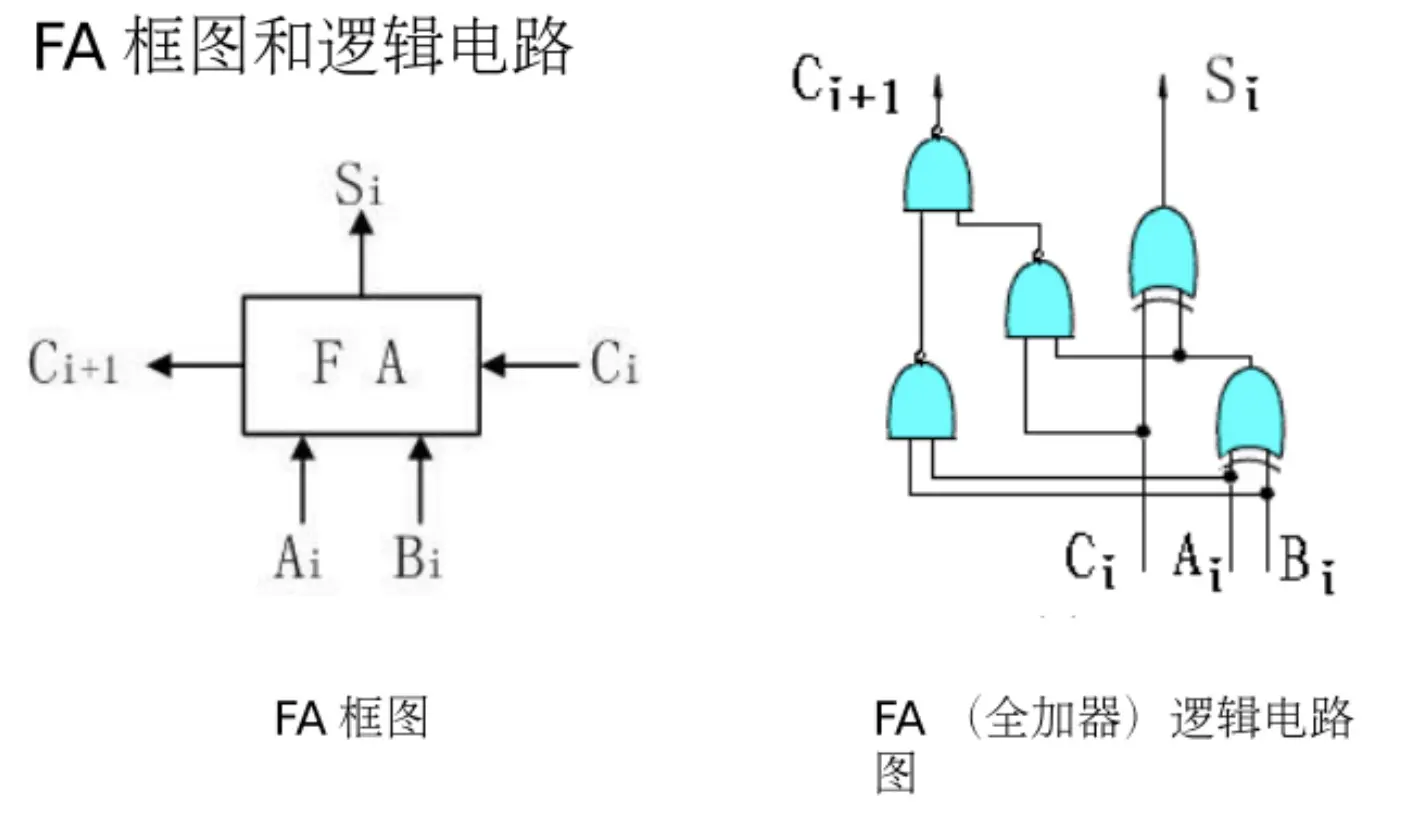
行波进位的补码加法减法器

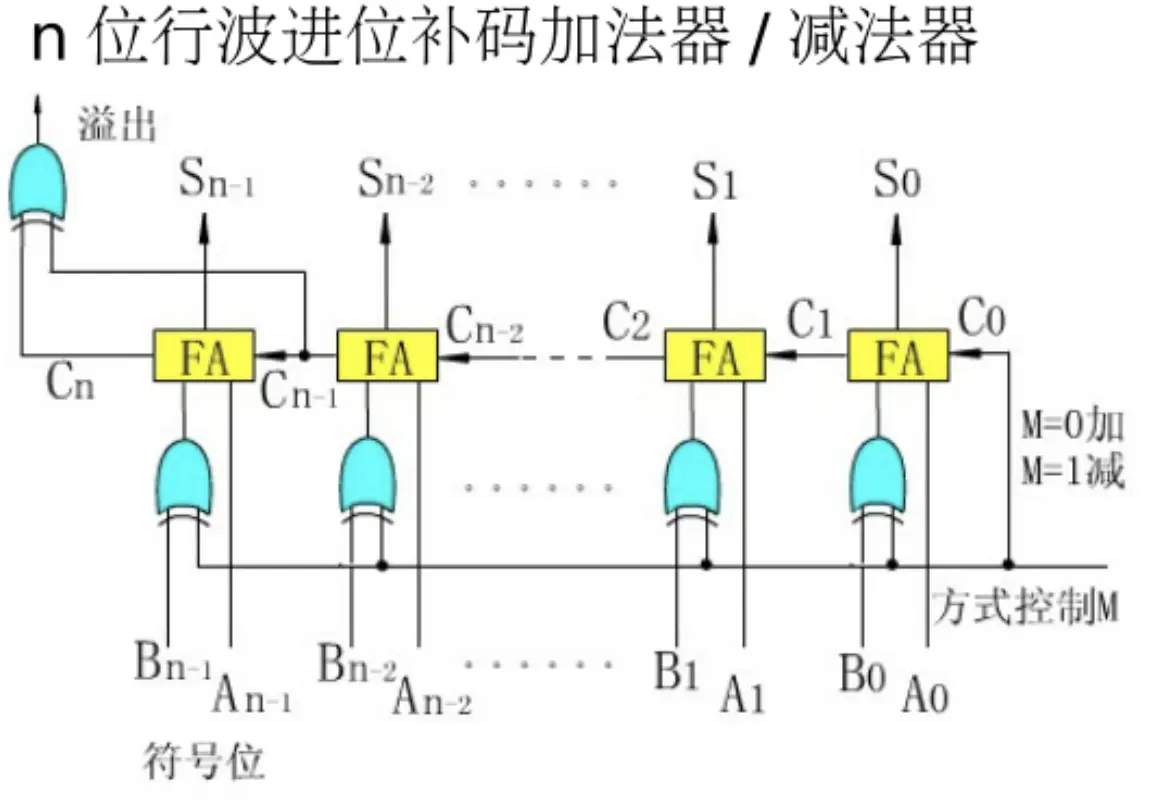
解题过程链接到标题

定点数链接到标题

例：求 $(-1100) + (-1000)$ 原数据与目标数据均用原码表示。

step1.判断两个操作数是否为补码形式表示，如果不是先求补，根据运算类型处理第二个操作数，是减法就求负数的补码；

$x=[-1100]_原=[110100]_补$

$y=[-1000]_原=[111000]_补$

step2.列竖式相加；

  110100
+ 111000
---------
  101100

step3.判断是否溢出；

$ovr=S_{f1}\oplus S_{f2}=1$ （发生负溢出）

step4.以题目所需要的形式表达结果。

$x+y=-0100$（发生负溢出）

浮点数链接到标题

例：求 ${0.52^2}_{10} + ({-0.43752^{3}}_{10})$ 。

step1.检查有无0操作数，有则无需计算；

step2.比较阶码大小并完成对阶；

小阶向大阶看齐

$x={0.52^2}_{10}={0.052^3}{10}={0100*2^3}{2}$

$y={-0.43752^{3}}_{10}={01112^{3}}_2$

step3.尾数加减；

  00100
+ 11001
--------
  11101

step4.规格化；

$x+y={-0.0011}_22^3={-0.1100}_22^1$

step5.舍入处理；

根据规格化右移时尾数域右端流出的数据来进行舍入，一般有以下四种舍入方法：

0 舍 1 入法：流出为 1 则向最低位增 1，否则不做处理；
恒舍法：无论流出的是什么都不做处理；
末位恒置 1 法：无论流出的是什么都将最低位置为 1；
查表舍入法：在 ROM 或 PLA 中存放下溢处理表，需要时查询该表判断如何舍入。

step6.判断是否溢出；

$ovr=\bar{A_f}\bar{B_f}S_f+A_fB_f\bar{S_f}=0$ 未发生溢出

浮点数的加减可能会造成以下四种溢出：

阶码上溢：超过了阶码可以表示的最大正指数，一般将这样的结果视为+∞或-∞；

阶码下溢：超过了阶码可以表示的最小负指数，一般将这样的结果视为0；

尾数上溢：两个同符号尾数相加产生了最高位向上的进位，要将尾数右移，阶码增 1 来重新对齐；

尾数下溢：在将尾数右移时，尾数的最低有效位从尾数域右端流出，要进行舍入处理。

step7.按题目要求处理结果各部分的编码形式，组装结果。

$x + y = {-0.1100}2*2^1 = {-1.5}{10} = {11011100}_2$

乘法运算链接到标题

汇编指令链接到标题

操作符	操作数	执行的操作	描述
MUL	SRC	(AX) <- (AL) * (SRC)	无符号乘法(byte)
MUL	SRC	(DX, AX) <- (AX) * (SRC)	无符号乘法(word)
IMUL	SRC	(AX) <- (AL) * (SRC)	带符号乘法(byte)
IMUL	SRC	(DX, AX) <- (AX) * (SRC)	带符号乘法(word)

以上指令均影响符号位，但对 CF、OF 外的符号位无定义。

对于 MUL 指令，如果乘积的高一半（即字节操作的 (AH) 或字操作的 (DX)）为 0，则 CF 和 OF 位均为 0，否则为 1。

这样的条件码设置可以用来检查字节相乘的结果是字节还是字，或者检查字相乘的结果是字还是双字。

MUL 指令只允许两个长度一致的数据进行计算，即允许 byte * byte、word * word，不允许 byte * word。

底层实现链接到标题

进行乘法运算的两个操作数是用原码形式存储的，硬件层面将乘法拆分为了多次加法。

浮点数运算规则链接到标题

$xy=2^{E_x+E_y}(M_x*M_y)$

硬件链接到标题

5 * 5 不带符号的阵列乘法器

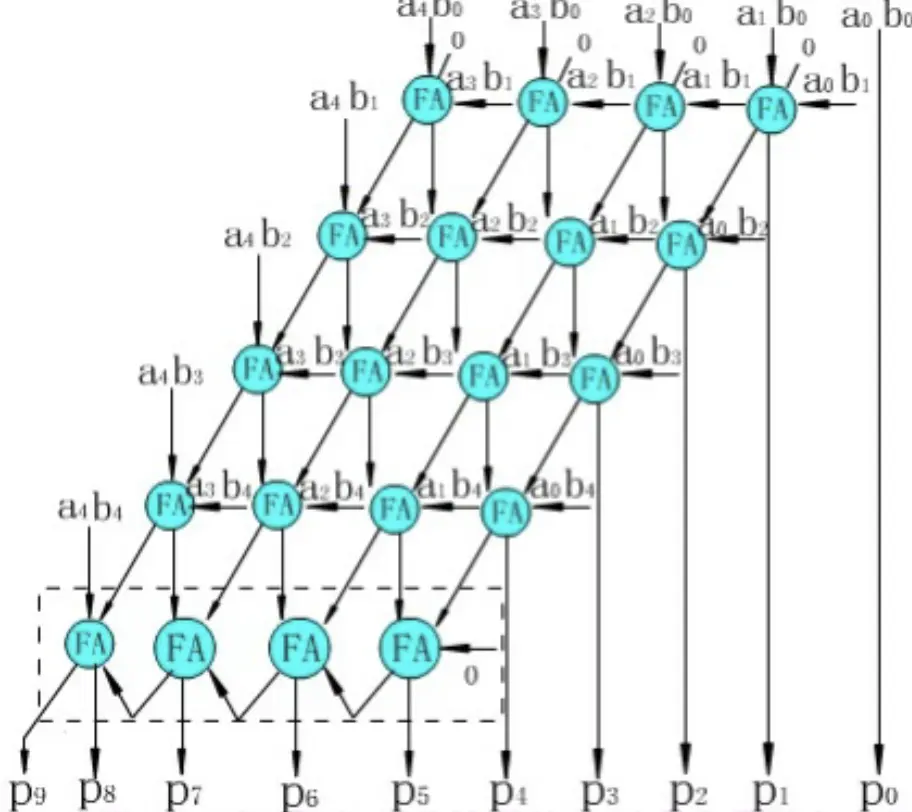
斜线为进位的输入与输出，直线为和的输出。

给阵列乘法器搭配一个被加数产生部件即可组合为不带符号的阵列乘法器

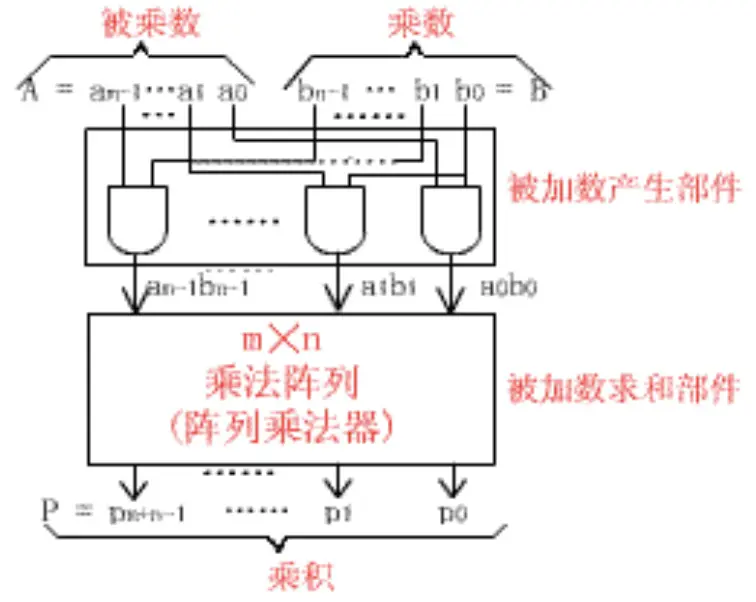
再搭配下面这个对 2 求补器

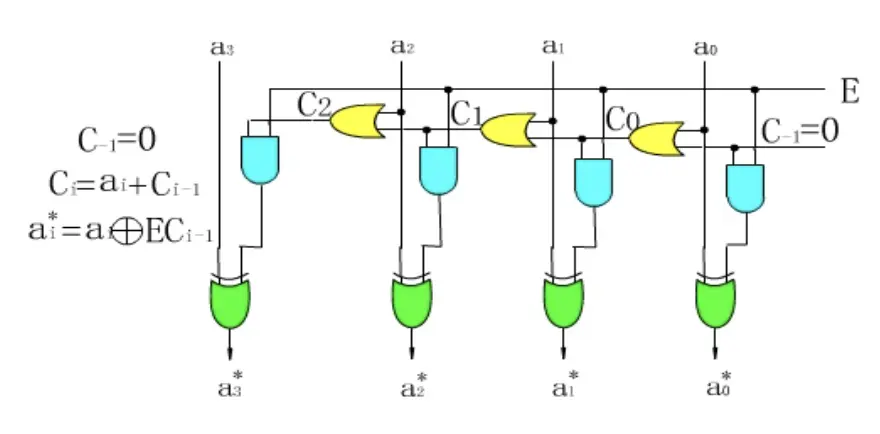
即可组装出带符号的阵列乘法器

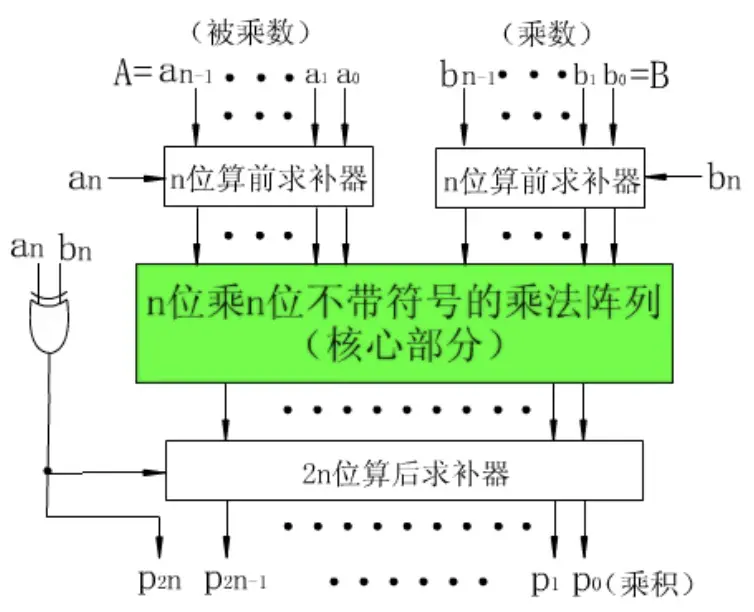
解题过程链接到标题

定点数链接到标题

例：求 $(01111) * (10011)$ 原数据与目标数据均用补码表示。

step1.判断两个操作数是否为原码形式表示，如果不是先求补；

$x=[01111]_补=[01111]_原$

$y=[10011]_补=[11101]_原$

step2.列竖式相乘；

      1111
x     1101
-------------
      1111
     0000
    1111
   1111
-------------
  11000011

step3.计算符号位；

$s_f = x_f\oplus y_f = 0 \oplus 1 = 1$

step4.以题目所需要的形式表达结果。

$x*y = {111000011}_原 = {100111101}_补$

浮点数链接到标题

例：求 ${0.5}{10} * {(-0.4375)}{10}$ 。

step1.检查有无0操作数，有则无需计算；

step2.写出尾码的原码形式，阶码的移码、补码形式；

$[M_x]_原=1000$

$[M_y]_原=0111$

$[E_x]移={-1}{10}=0011$

$[E_y]移={-2}{10}=0010$

$[E_y]_补=1110$

step3.阶码运算；

阶码运算需要用到两位符号位，而之前的约定里 8bit 的浮点数显然放不下这么大的数据，所以下面的计算选择扩大数据长度进行。

${E_x+E_y}=0011+1110=0001={[001]}_补$

step4.尾数处理；

$M_xM_y=10001110=1110000$

由于只需要 4 位有效数字，因此将结果修正为 $1.110(000)*2^{-3}=0.1110(000)*2^{-2}$ 。

step5.规格化与溢出检查、舍入处理；

该结果满足规格化，且未发生溢出，结果为 $0.1110*2^{-2}$ 。

step6.确定积的符号，组装结果。

$s_f = x_f\oplus y_f = 0 \oplus 1 = 1$

$x * y = {10101100}_2$

除法运算链接到标题

汇编指令链接到标题

操作符	操作数	执行的操作	描述
DIV	SRC	(AL) <- (AL) / (SRC) 的商	无符号除法(byte)
		(AH) <- (AL) / (SRC) 的余数	无符号除法(byte)
DIV	SRC	(AX) <- (AX) / (SRC) 的商	无符号除法(word)
		(DX) <- (AL) / (SRC) 的余数	无符号除法(word)
IDIV	SRC	(AL) <- (AL) / (SRC) 的商	带符号除法(byte)
		(AH) <- (AL) / (SRC) 的余数	带符号除法(byte)
IDIV	SRC	(AX) <- (AX) / (SRC) 的商	带符号除法(word)
		(DX) <- (AL) / (SRC) 的余数	带符号除法(word)

以上指令均影响符号位，但无定义。

如果字节操作时被除数的高 8 位 $\geq$ 除数的绝对值，或字操作时被除数的高 16 位 $\geq$ 除数的绝对值，商会产生溢出。

DIV 指令只允许 double word / word、word * byte，不允许相同长度的数据进行计算。

底层实现链接到标题

进行除法运算的两个操作数是用原码形式存储的，硬件层面将除法拆分为了多次加法与减法。

浮点数运算规则链接到标题

$x/y=2^{E_x-E_y}*(M_x/M_y)$

硬件链接到标题

可控加法/减法单元 CAS

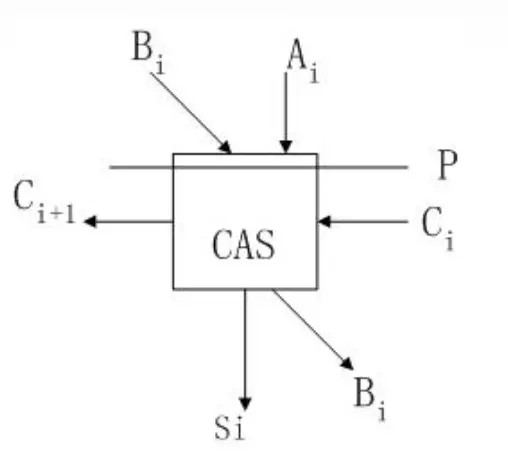
P = 0 时 CAS 做加法运算，P = 1 时 CAS 做减法运算。

用多个 CAS 组装即可成为 4 位除 4 位阵列除法器

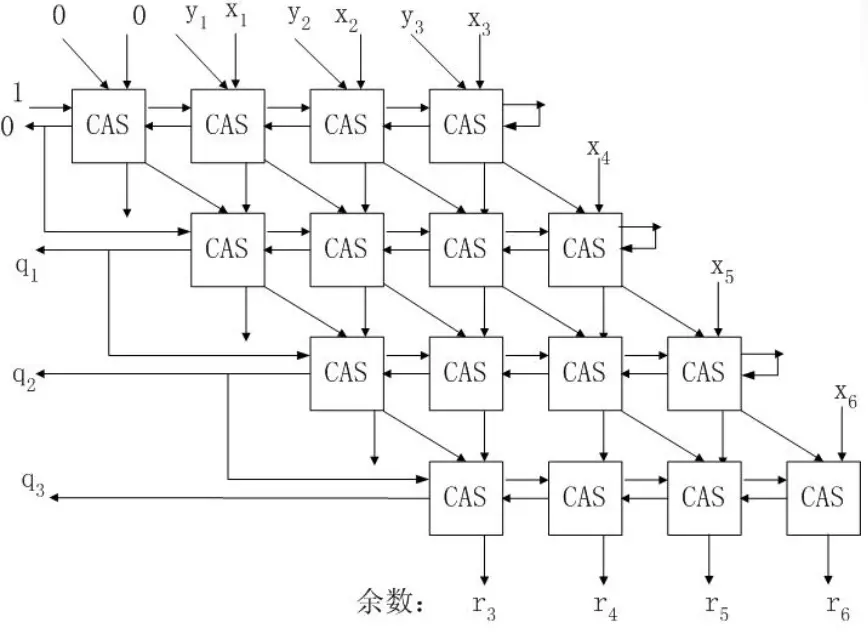
解题过程链接到标题

定点数链接到标题

除法要求被除数的绝对值小于输出的。

例子

例：求 $(0.1001) / (0.1011)$ 。

step1.求出两个操作数绝对值的原码、补码；

$\lvert x \rvert =[001001]_原=[000111]_补$

$\lvert y \rvert =[001011]_原=[001011]_补$

$-\lvert y \rvert =[111011]_原=[110101]_补$

step2.判断是否溢出；

$\lvert x \rvert < \lvert y \rvert$ 没溢出

step3.被除数减去除数；

step4.若所得余数为正，则上商为 1，余数左移一位，减去除数；若所得余数为负，则上商为 0，余数左移一位，加上除数；

step5.重复第 4 步，直到求得需要的商的各位为止；

一般商的长度与输出的位数一致。

step6.若最后一次所得余数为负，则需再加一次除数以恢复余数；

上面四步的过程如下：

  001001
- 110101
-----------------
  111110   0
<-111100
+ 001011
-----------------
  000111   0.1
<-001110 
- 110101
-----------------
  000011   0.11
<-000110
- 110101
-----------------
  111011   0.110
<-110110
+ 001011
-----------------
  000001   0.1101

$x / y 的商 = 0.1101_2 余数 = 0.00,000,001$

step7.计算结果的符号；

商的符号为被除数与除数的符号异或结果，余数的符号与被除数一致。

$商_f = x_f\oplus y_f = 0 \oplus 0 = 0$

${余数}_f = x_f = 0$

step8.以题目所需要的形式表达结果。

浮点数链接到标题

例：求 ${0.5}{10}/{-0.9375}{10}$ 。

step1.检查有无0操作数，有则无需计算；

step2.写出尾码的原码、补码形式，阶码的移码、补码形式；

$\lvert M_x \rvert=[001000]_原=[001000]_补$

$\lvert M_y \rvert=[001111]_原=[001111]_补$

$-\lvert M_y \rvert=[111111]_原=[110001]_补$

$[E_x]移={-1}{10}=0011$

$[E_y]移={-1}{10}=0011$

$[E_y]_补=1111$

$[-E_y]_补=0001$

step3.阶码运算；

${E_x+E_y}=0011+0001=0110={[100]}_补$

step4.尾数处理；

$M_x / M_y=001000/001111=0.1000$

余数为 $0.00001$

step5.规格化与溢出检查、舍入处理；

该结果满足规格化，且未发生溢出，结果为 $0.1000$ 。

step6.确定积的符号，组装结果。

$s_f = x_f\oplus y_f = 0 \oplus 1 = 1$

$x / y = {11001000}_2$

逻辑运算链接到标题

操作符	操作数	执行的操作	描述
AND	DST, SRC	(DST) <- (SRC) $\land$ (DST)	逻辑与
OR	DST, SRC	(DST) <- (SRC) $\lor$ (DST)	逻辑或
NOT	OPR	(OPR) <- ($\overline{OPR}$)	逻辑非
XOR	DST, SRC	(DST) <- (DST) $\oplus$ (SRC)	异或
TEST	OPR1, OPR2	(OPR1) $\wedge$ (OPR2)	测试

NOT 不影响标志位，其他 4 种指令会使 CF 和 OF 位为 0，AF 位无定义，CF、SF、PF 会根据运算结果设置。

位运算链接到标题

操作符	操作数	描述
SHL	OPR, CNT	逻辑左移
SAL	OPR, CNT	算术左移
SHR	OPR, CNT	逻辑右移
SAR	OPR, CNT	算术右移
ROL	OPR, CNT	循环左移
RCL	OPR, CNT	带进位的循环左移
ROR	OPR, CNT	循环右移
RCR	OPR, CNT	带进位的循环右移

执行的操作如下图所示：

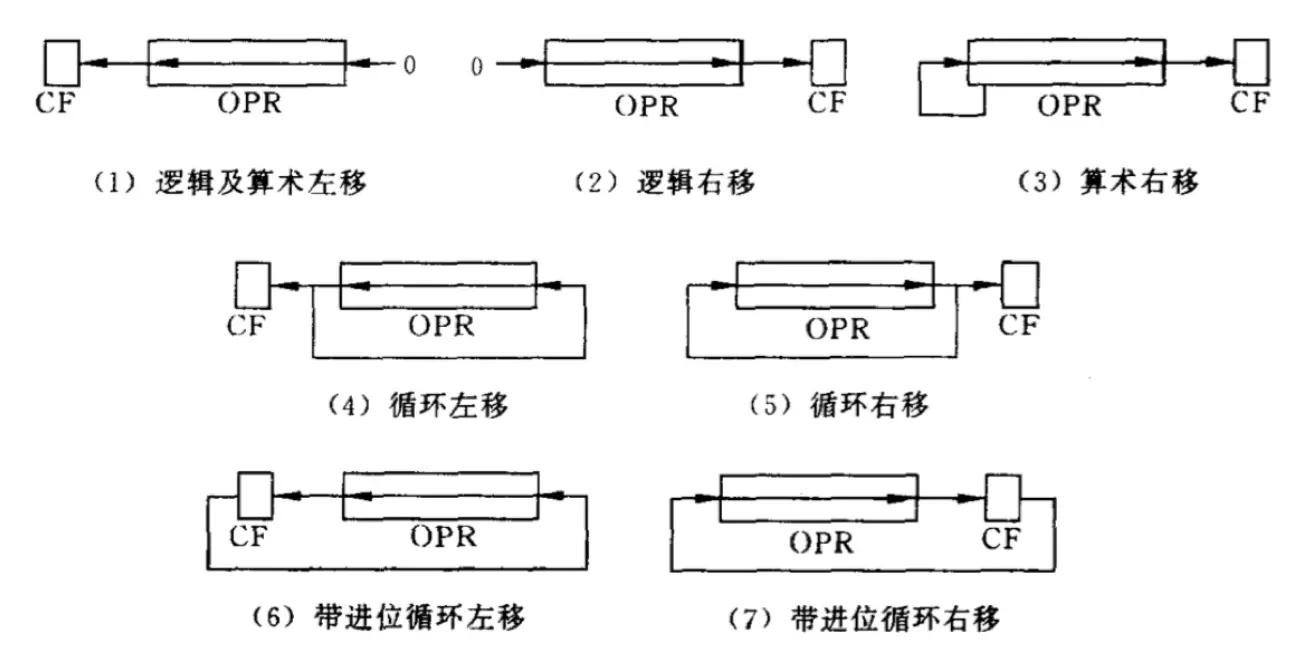
CNT 在 8086 上可以是 1 或 CL(所需移动的位数大于 1 时)。

OF位只有当 CNT=1 时才是有效的，否则该位无定义。当 CNT=1 时，在移位后最高有效位的值发生变化时(原来为 0，移位后为 1；或原来为1，移位后为0）0F 位置 1，否则置 0。循环移位指令不影响除 CF 和 OF 以外的其他条件标志。而移位指令则根据移位后的结果设置 SF、ZF 和 PF 位，AF 位则无定义。

约定 链接到标题

加、减法运算 链接到标题

汇编指令 链接到标题

对以字为单位的数据进行计算 链接到标题

底层实现 链接到标题

公式 链接到标题

溢出检验 链接到标题

硬件 链接到标题

解题过程 链接到标题

定点数 链接到标题

浮点数 链接到标题

乘法运算 链接到标题

汇编指令 链接到标题

底层实现 链接到标题

浮点数运算规则 链接到标题

硬件 链接到标题

解题过程 链接到标题

定点数 链接到标题

浮点数 链接到标题

除法运算 链接到标题

汇编指令 链接到标题

底层实现 链接到标题

浮点数运算规则 链接到标题

硬件 链接到标题

解题过程 链接到标题

定点数 链接到标题

浮点数 链接到标题

逻辑运算 链接到标题

位运算 链接到标题

约定链接到标题

加、减法运算链接到标题

汇编指令链接到标题

对以字为单位的数据进行计算链接到标题

底层实现链接到标题

公式链接到标题

溢出检验链接到标题

硬件链接到标题

解题过程链接到标题

定点数链接到标题

浮点数链接到标题

乘法运算链接到标题

汇编指令链接到标题

底层实现链接到标题

浮点数运算规则链接到标题

硬件链接到标题

解题过程链接到标题

定点数链接到标题

浮点数链接到标题

除法运算链接到标题

汇编指令链接到标题

底层实现链接到标题

浮点数运算规则链接到标题

硬件链接到标题

解题过程链接到标题

定点数链接到标题

浮点数链接到标题

逻辑运算链接到标题

位运算链接到标题