这是 Reach-Top 4654 题的题解,翻译自 Codeforces。
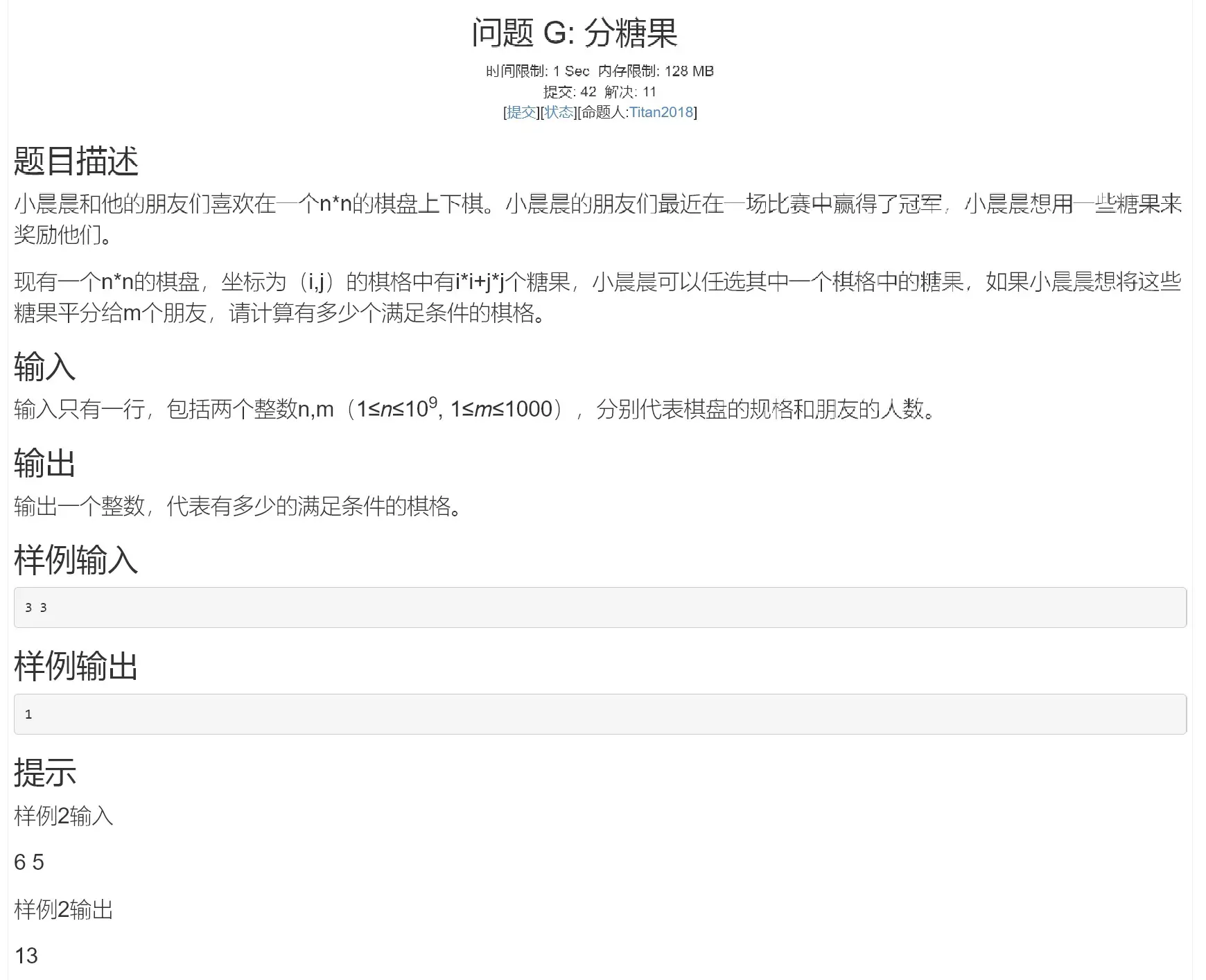
本题应用了一些取余的运算法则,值得写一篇博客总结一下。
数学前提 链接到标题
取模运算与取余运算的区别 链接到标题
这两者都是只针对整型数的运算,有以下两步组成:
- 求整数商: c = [a / b];
- 计算模或余数: r = a - c * b;
而两者的区别是在第一步的处理方法上:
- 取余运算: c = fix(a / b);
- 取模运算: c = floor(a / b);
由此我们可知取余运算在计算c的值时是向0方向舍入的,而取模运算在计算c的值时是向负无穷方向舍入的。
显然两者在非负情况下结果都是一样的,但在负数情况下是有区别的,我们可以由以下情形来得到更好的体感:
例1: 计算 -7 Mod 4 链接到标题
- a = -7; b = 4;
- 取余运算:
- c = fix(a / b) = fix(-7 / 4) = -1;
- r = a - c * b = -7 - (-1) * 4 = -3;
- 取模运算:
- c = floor(a / b) = floor(-7 / 4) = -2;
- r = a - c * b = -7 - (-2) * 4 = 1;
例2: 计算 7 Mod 4 链接到标题
- a = 7; b = 4;
- 取余运算:
- c = fix(a / b) = fix(7 / 4) = 1;
- r = a - c * b = 7 - 1 * 4 = 3;
- 取模运算:
- c = floor(a / b) = floor(7 / 4) = 1;
- r = a - c * b = 7 - 1 * 4 = 3;
例3: 计算 7 Mod -4 链接到标题
- a = 7; b = -4;
- 取余运算:
- c = fix(a / b) = fix(7 / -4) = -1;
- r = a - c * b = 7 - (-1) * (-4) = 3;
- 取模运算:
- c = floor(a / b) = floor(7 / -4) = -2;
- r = a - c * b = 7 - (-2) * (-4) = -1;
例4: 计算 -7 Mod -4 链接到标题
- a = -7; b = -4;
- 取余运算:
- c = fix(a / b) = fix(-7 / -4) = 1;
- r = a - c * b = -7 - 1 * (-4) = -3;
- 取模运算:
- c = floor(a / b) = floor(-7 / -4) = 1;
- r = a - c * b = -7 - 1 * (-4) = -3;
归纳:当 a 和 b 正负号一致时,求模运算和求余运算所得的c的值一致,因此结果一致。
当正负号不一致时,结果不一样。
不同环境下%运算符的含义 链接到标题
- %为求余运算符的环境: c/c++、java、JavaScript、Golang
- %为取模运算符的环境: Python
因为题目是要求使用 c++ 解题的,所以解下来的讨论我们都认为 % 是求余运算符。
基础法则 链接到标题
加法: 链接到标题
- $(a + b) \mod p = (a \mod p + b \mod p) \mod p$
- $(a + p) \mod p = a \mod p$
减法: 链接到标题
- $(a - b) \mod p = (a \mod p - b \mod p)\mod p$
- $(a - b + p)\mod p = (a - b) \mod p$
乘法: 链接到标题
- $(a * b)\mod p = (a\mod p * b\mod p)\mod p$
- 逆元:$[(a * b \mod p) * (b^{−1} \mod p)]\mod p = a \mod p$
结合律: 链接到标题
- $[(a + b) \mod p + c] \mod p = [a + (b + c) \mod p]\mod p$
- $[(a * b) \mod p * c] \mod p = [a * (b * c) \mod p]\mod p$
交换律: 链接到标题
- $(a + b) \mod p = (b + a) \mod p$
- $(a * b) \mod p = (b * a) \mod p$
分配律: 链接到标题
- $(a + b) \mod p = (a \mod p + b \mod p) \mod p$
- $[(a + b) \mod p * c] \mod p = [(a * c) \mod p + (b * c) \mod p] \mod p$
- $d \mod (a * b * c) = (d \mod a) + a[(d$ \ $a) \mod b] + a * b [(d$ \ $a$ \ $b) \mod c]$,符号 \ 是欧几里德除法中的除法操作符,运算结果为整数商
- $c \mod (a + b) = (c \mod a) + [b * c$ \ $(a + b)] \mod b - [b * c$ \ $(a + b)] \mod a$.
乘方: 链接到标题
- $a^b \mod p = [(a \mod p)^b] \mod p$
累加: 链接到标题
- $\Big( \displaystyle \sum^{n} _ {1}{x} \Big) \mod p = \Big( \displaystyle \sum^{n} _ {1}{x} \mod p \Big) \mod p$
一些说明: 链接到标题
同余式: 链接到标题
正整数 a,b 对 p 取模,它们的余数相同,记作 $a\equiv b(mod \ p)$。
符号: 链接到标题
$n \mod p$ 得到结果的正负由被除数 n 决定,与 p 无关。样例可见上文的四个样例。
模逆元: 链接到标题
也称为模倒数,或者模逆元。一整数 a 对同余 n 之模逆元是指满足以下公式的整数 b
$a^{-1} \equiv b \pmod n$
也可以写成以下的式子
$a * b \equiv 1 \pmod n$.
费马小定理: 链接到标题
假如 a 是一个整数,p 是一个质数,那么 $a^{p}-a$ 是 p 的倍数,可以表示为
$a^p \equiv a \pmod p$
如果 a 不是 p 的倍数,这个定理也可以写成更加常用的一种形式
$a^{p-1} \equiv 1 \pmod p$
ps:同余还有很多很多的知识,但不和本篇博客的内容大多无关,我们只需了解上面介绍的费马小定理即可,其他的以后有机会再总结(挖坑+1)。
恒等式 链接到标题
- $(a \mod p) \mod p = a \mod p$
- 对所有的正数 x 有:$p^x \mod p = 0$
- 如果 p 是一个质数,且不为 b 的因数,此时由费马小定理有:$a * b^{p−1} \mod p = a \mod p$
逆运算 链接到标题
- $[(−a \mod p) + (a \mod p)] \mod p = 0$
- $b^{−1} \mod p$ 表示模反元素。当且仅当 b 与 n 互质时,等式左侧有定义:$[(b^{−1} \mod p) * (b \mod p)] \mod p = 1$。
除法 链接到标题
b 与 p 互质时有:$\frac{a}{b} \mod n = [(a \mod p) * (b^{−1} \mod p)] \mod p$
应用 链接到标题
有了上面那么多数学知识作为基础后,解这题就变得十分简单了。
分析数据 链接到标题
100m 的数据,显然最多只能用一重循环,而变量有 i 和 j 两个,那么首要目标就是找出 i 和 j 的关系了。
由题干可知 i 和 j 的平方和应该是 m 的倍数,即满足这这样一个式子:
$(i^2 + j^2) \mod m = 0$
再利用分配律可以得到:
$(i^2 \mod m + j^2 \mod m) \mod m = 0 (*)$
我们可以利用 $*$ 式设计出算法来解题了
初始化 链接到标题
我们利用取余的乘法法则再对 $*$ 式做一步处理,得到:
$[(i \mod m * i \mod m) \mod m + (j \mod m * j \mod m) \mod m] \mod m = 0$
由此可知 i 和 j 是以 m 为周期出现的,那么我们只需要计算 1 - m 这样一个循环中 $i^2 \mod m$ 出现了几次就可以将 n 的数据压缩为 m 个了。
这里有一点需要注意的是,最后一个循环有可能是不完整的循环,需要特殊处理一下。
计算结果 链接到标题
将 $i^2 \mod m$ 的出现次数以 $i^2 \mod m$ 为下标存到一个数组 vis 后,我们就可以开始着手利用 $*$ 式计算结果了。
我们令 $i^2 \mod m$ 为 $a$ , $j^2 \mod m$ 为 $b$ ,那么 $(a + b) \mod m = 0$ 又 $0 \leq a , b < m$ ,所以只需要计算 $vis[a] * vis[m - a]$ 即可计算一组合适的 i 和 j 的个数。
这里也有一个需要特殊处理的点,就是 i 和 j 都能被 m 整除的情况,所以加上 $vis[0] * vis[0]$ 就可以得到最终答案了。
代码 链接到标题
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1009;
long long n, m, vis[maxn], ans;
int main() {
cin >> n >> m;
for (int i = 1; i <= m; i++) {
vis[i * i % m] += n / m;
}
for (int i = 1; i <= n % m; i++) {
vis[i * i % m]++;
}
for (int i = 1; i < m; i++) {
ans += vis[i] * vis[m - i];
}
ans += vis[0] * vis[0];
cout << ans;
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int main() {
long long m, n;
vector<int> v[1005];
int y[1005];
scanf("%lld%lld", &n, &m);
for (int i = 0; i < m; i++) {
v[(i * i) % m].push_back(i);
y[i] = (i * i) % m;
}
long long ans = 0;
for (int i = 0; i < m; i++) {
int k = (m - y[i]) % m;
for (int j = 0; j < v[k].size(); j++) {
ans += (n / m + (((n % m) >= i) && i > 0)) * (n / m + (((n % m) >= v[k][j]) && v[k][j] > 0));
}
}
printf("%lld\n", ans);
return 0;
}